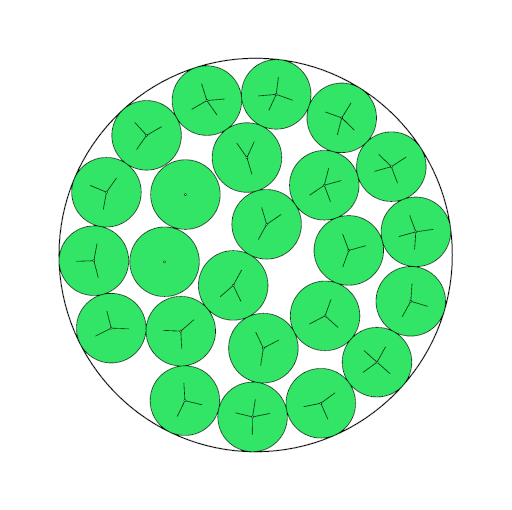
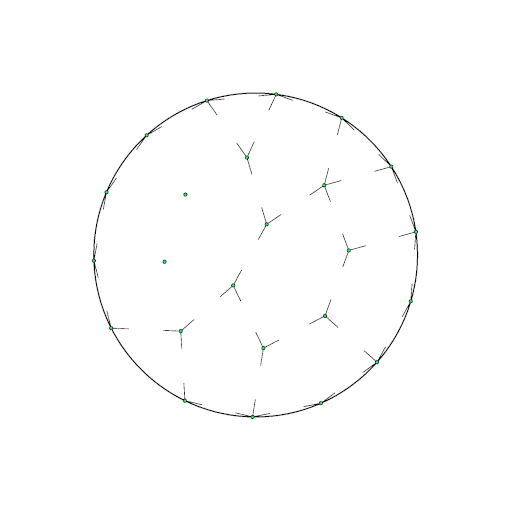
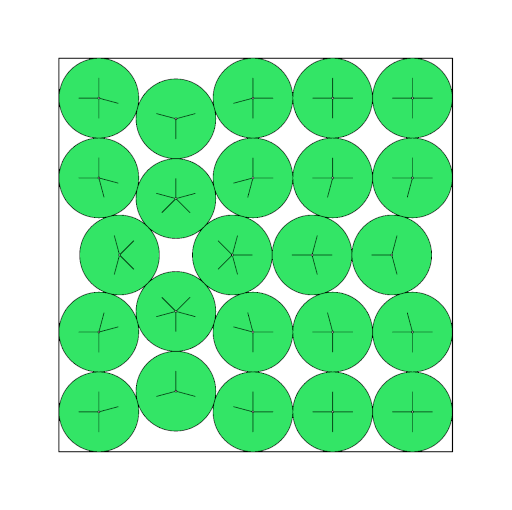
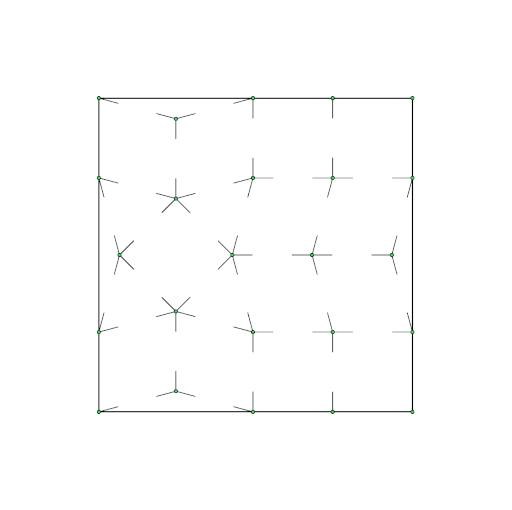
Equivalence between circle packing and point packing
In the following two pictures, a packing of 24 circles (left) and a packing of 24 points (right), both in a square are shown.
Both packings are related by the fact that the circle centers in the left picture match exactly with the points in the right
picture. So you can think of a point packing as of a packing of circles with zero radii, or, with other words, by shrinking
the container by one circle radius. This is true since a square-shaped container preserves its shape when it is cropped with
equal width around it.
The same holds for a circular container, see next two pictures. (Beware: this is not true for a rectangular container!)